Grado
5

Adivina mi regla: locura de multiplicación

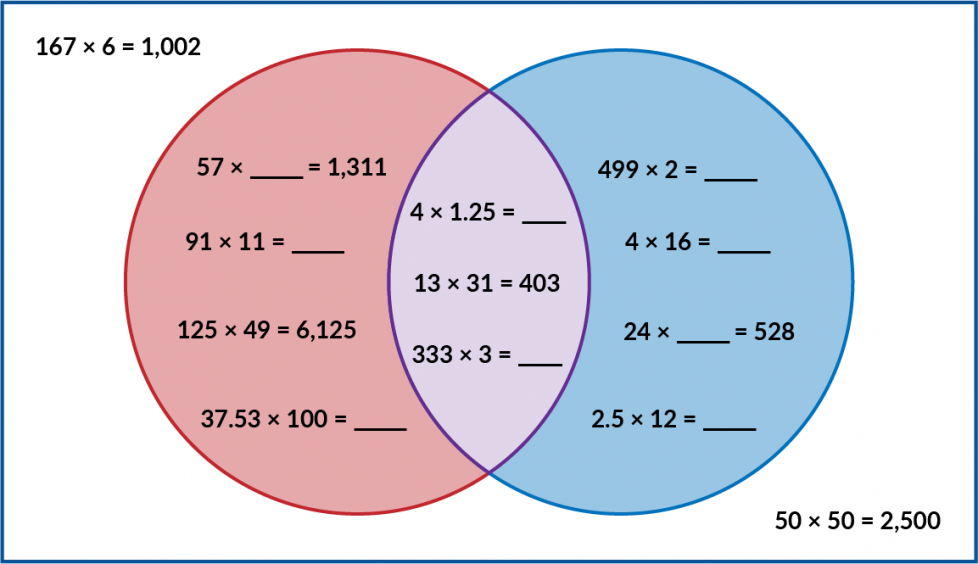
Un círculo rojo y uno azul se traslapan. Dentro del círculo rojo: 57 por espacio en blanco = 1311. 91 por 11 = espacio en blanco. 125 veces 49 = 6125. 37.53 por 100 = espacio en blanco. Dentro del círculo azul: 499 por 2 = espacio en blanco. 4 por 16 = espacio en blanco. 24 por espacio en blanco = 528. 2.5 por 12 = espacio en blanco. Donde los círculos se traslapan: 4 por 1.25 igual a espacio en blanco. 13 por 31 = 403. 333 por 3 igual a espacio en blanco. Afuera de los círculos: 167 por 6 = 1002. 50 por 50 = 2500.
  1. Hay reglas para decidir qué ecuaciones pertenecen en los círculos. Resuelve las ecuaciones y úsalas para determinar las reglas. ¿Cuál es la regla para estar en el círculo rojo? ¿Cuál es la regla para estar en el círculo azul?
  2. ¿Cuál es la regla para estar en la intersección de ambos círculos?
  3. ¿Cuál es otra expresión que pertenece solo en el círculo rojo?
  4. ¿Cuál es otra expresión que pertenece solo en el círculo azul?

Comienza por hallar los productos de 91 × 11 en el círculo rojo, 499 × 2 en el círculo azul y 333 × 3 en la intersección de los círculos. ¿En qué se parecen esos productos? ¿En qué son diferentes?

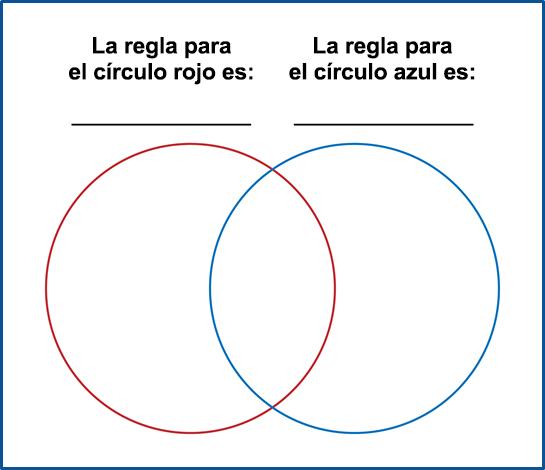
Haz tu propia regla que involucre multiplicación. Puedes usar los círculos de abajo o dibujarlos. Si es posible, muestra algunos ejemplos que pertenezcan en el interior de cada círculo y algunos ejemplos que no pertenezcan en ningún círculo.

Un círculo rojo y uno azul se traslapan. Cada círculo tiene un encabezado. La regla para el círculo rojo es... La regla para el círculo azul es...
Versión para imprimir

Google doc para imprimir y copiar

Referencia para los educadores

Ejemplos de problemas y sus soluciones