Las matemáticas en nuestro mundo: la Reductora automática
Cameron acaba de inventar la Reductora automática. ¡Reduce o encoge objetos durante 1 hora! Miras a través de ella como con una cámara, presionas uno de los botones rojos con fracciones, después presionas el botón con la X para multiplicar y —¡BUM! — lo que sea a lo que estabas apuntando se encoge.
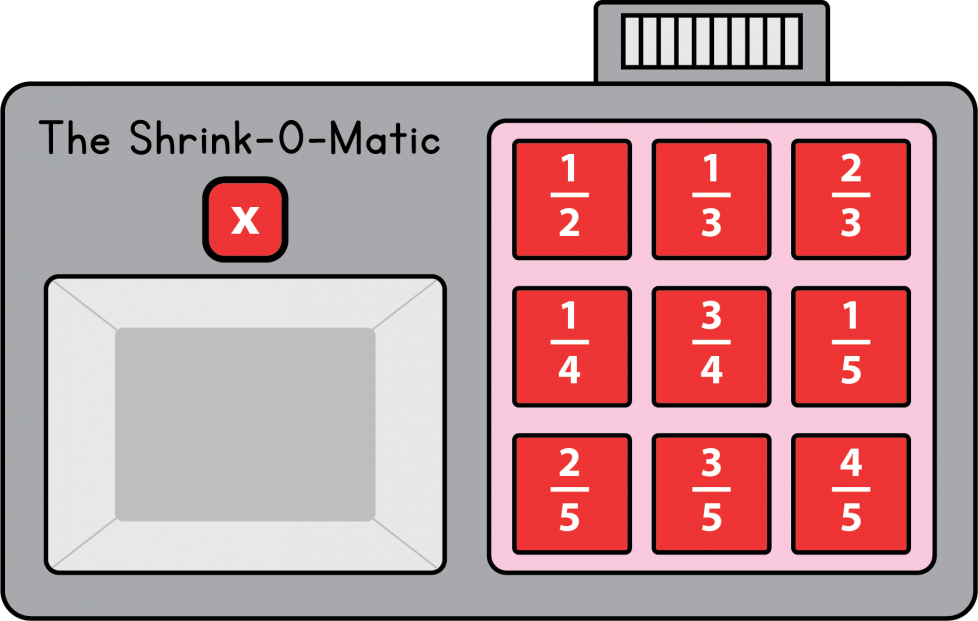
La fracción que presiones determina el nuevo tamaño del objeto.
Cameron dijo: "Si apuntaras con la Reductora automática a una escalera de 12 pies de altura y presionaras el botón de ⅓, se encogería a ⅓ de su tamaño original. Dado que ⅓ de 12 es 4, ahora tendrías una escalera de 4 pies de altura."
Está emocionado con probar su nuevo invento y comenzó a hacer una lista de cosas que podría encoger.
| Objeto | Tamaño original aproximado |
|---|---|
| Columpio | 10 pies de alto |
| Camión de bomberos | 35 pies de largo |
| Árbol de manzanas | 30 pies de largo |
| Rascacielos | 300 pies de alto |
| Su casa | 24 pies de alto |
| Un avión | 180 pies de largo |
- Usa dibujos, modelos o números para mostrar qué está sucediendo.
- ¿Qué ves? ¿Qué te preguntas?
- ¿Qué preguntas matemáticas puedes hacer sobre esta situación? ¡Responde todas las preguntas que puedas!
- Puedes encoger un objeto hasta la ½ de su tamaño original dividiendo entre 2. ¿Cómo puede ayudarte esta información para determinar el tamaño de un objeto encogido a ⅓, ¼ o ⅕ de su tamaño?
- ¿Cómo conocer ⅓ del tamaño te ayuda a determinar ⅔ del tamaño?
- Muéstrale tu trabajo a alguien más y explícale tu razonamiento. ¿Entendió?
- ¡Pregúntale si tiene alguna otra pregunta que pudieras responder!
Si encoges a toda tu familia a ⅕ de su tamaño original, ¿qué estatura tendría cada uno? Dibuja a cada miembro de tu familia miniatura y recórtalos. ¿Qué clases de aventuras tendrían?
Google doc para imprimir y copiar
Ejemplos de problemas y sus soluciones